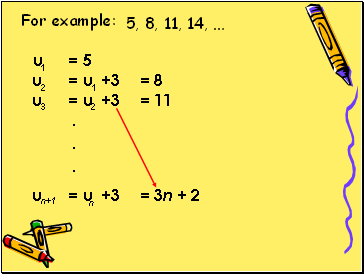Sequences - Finding a rule

Page
1

Slide 1

Sequences

Slide 2

A sequence is a set of terms, in a definite order, where the terms are obtained by some rule.

A finite sequence ends after a certain number of terms.

An infinite sequence is one that continues indefinitely.

Slide 3

For example:

1, 3, 5, 7, …

(This is a sequence of odd numbers)

1st term = 2 x 1 – 1 = 1

2nd term = 2 x 2 – 1 = 3

3rd term = 2 x 3 – 1 = 5

nth term = 2 x n – 1 = 2n - 1

. .

. .

. .

+ 2

+ 2

Slide 4

Notation

1st term = u

2nd term = u

3rd term = u

nth term = u

. .

. .

. .

1

2

3

n

Slide 5

OR

1st term = u

2nd term = u

3rd term = u

nth term = u

. .

. .

. .

0

1

2

n-1

Slide 6

Finding the formula for the terms of a sequence

Slide 7

A recurrence relation defines the first term(s) in the sequence and the relation between successive terms.

Slide 8

u = 5

u = u +3 = 8

u = u +3 = 11

u = u +3 = 3n + 2

.

.

.

1

2

3

n+1

For example:

5, 8, 11, 14, …

1

2

n

Slide 9

What to look for

when looking for the rule

defining a sequence

Slide 10

Constant difference: coefficient of n is the difference

2nd level difference: compare with square numbers

(n = 1, 4, 9, 16, …)

3rd level difference: compare with cube numbers

(n = 1, 8, 27, 64, …)

None of these helpful: look for powers of numbers

(2 = 1, 2, 4, 8, …)

Signs alternate: use (-1) and (-1)

-1 when k is odd +1 when k is even

k

k

2

3

n - 1

Slide 11

EXAMPLE:

Find the next three terms in the sequence 5, 8, 11, 14, …

Slide 12

EXAMPLE:

The nth term of a sequence is given by x =

Find the first four terms of the sequence.

b) Which term in the sequence is ?

c) Express the sequence as a recurrence relation.