Cones and pyramids

Page
1

Slide 1

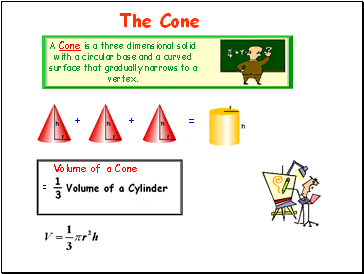
The Cone

A Cone is a three dimensional solid with a circular base and a curved surface that gradually narrows to a vertex.

Volume of a Cone

Slide 2

Find the volume of a cylinder with a radius r=1 m and height h=2 m. Find the volume of a cone with a radius r=1 m and height h=1 m

Volume of a Cylinder = base x height = pr2h

= 3.14(1)2(2)

= 6.28 m3

Exercise #1

Volume of a Cone = (1/3) pr2h

= (1/3)(3.14)(1)2(2)

= 2.09 m3

Slide 3

Find the area of a cone with a radius r=3 m and height h=4 m.

Use the Pythagorean Theorem to find l

l 2 = r2 + h2

l 2= (3)2 + (4)2

l 2= 25

l = 5

Surface Area of a Cone

Surface Area of a Cone

= pr2 + prl

= 3.14(3)2 + 3.14(3)(5)

= 75.36 m2

r = the radius h = the height l = the slant height

Slide 4

Textbook:

P. 421 - 422 # 2a, 3b, 9

P. 439 – 441 # 2abcd, 3, 4c, 5ab, 10abc

Cones – Practice Questions

Slide 5

A Pyramid is a three dimensional figure with a regular polygon as its base and lateral faces are identical isosceles triangles meeting at a point.

Pyramids

base = quadrilateral

base = pentagon

base = heptagon

Identical isosceles triangles

Slide 6

Volume of a Pyramid:

V = (1/3) Area of the base x height

V = (1/3) Ah

Volume of a Pyramid = 1/3 x Volume of a Prism

Volume of Pyramids

+

+

=

Slide 7

Find the volume of the pyramid. height h = 8 m apothem a = 4 m side s = 6 m

Area of base = ½ Pa

Exercise #2

h

a

s

Volume = 1/3 (area of base) (height)

= 1/3 ( 60m2)(8m)

= 160 m3

= ½ (5)(6)(4)

= 60 m2

Slide 8

Surface Area

= area of base

+ 5 (area of one lateral face)

Area of Pyramids

Find the surface area of the pyramid. height h = 8 m apothem a = 4 m side s = 6 m

h

a

s

Area of a pentagon

l

What shape is the base?

= ½ Pa

= ½ (5)(6)(4)

= 60 m2

Slide 9

Area of Pyramids

Find the surface area of the pyramid. height h = 8 m apothem a = 4 m side s = 6 m

h

a

s

Area of a triangle = ½ base (height)