Factoring Trinomials

Page
1

Slide 1

Factoring Trinomials

Slide 2

Multiply. (x+3)(x+2)

x • x + x • 2 + 3 • x + 3 • 2

Multiplying Binomials (FOIL)

F

O

I

L

= x2+ 2x + 3x + 6

= x2+ 5x + 6

Distribute.

Slide 3

x + 3

x

+

2

Using Algebra Tiles, we have:

= x2 + 5x + 6

Multiplying Binomials (Tiles)

Multiply. (x+3)(x+2)

Slide 4

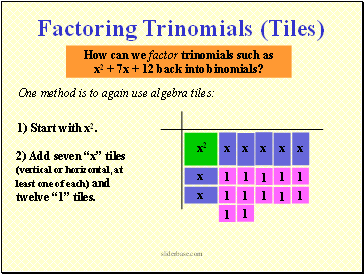
How can we factor trinomials such as

x2 + 7x + 12 back into binomials?

One method is to again use algebra tiles:

1) Start with x2.

Factoring Trinomials (Tiles)

2) Add seven “x” tiles (vertical or horizontal, at least one of each) and twelve “1” tiles.

Slide 5

How can we factor trinomials such as

x2 + 7x + 12 back into binomials?

One method is to again use algebra tiles:

1) Start with x2.

Factoring Trinomials (Tiles)

2) Add seven “x” tiles (vertical or horizontal, at least one of each) and twelve “1” tiles.

3) Rearrange the tiles until they form a rectangle!

We need to change the “x” tiles so the “1” tiles will fill in a rectangle.

Slide 6

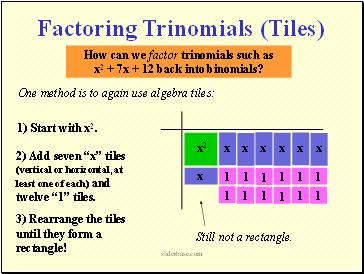
How can we factor trinomials such as

x2 + 7x + 12 back into binomials?

One method is to again use algebra tiles:

1) Start with x2.

Factoring Trinomials (Tiles)

2) Add seven “x” tiles (vertical or horizontal, at least one of each) and twelve “1” tiles.

3) Rearrange the tiles until they form a rectangle!

Still not a rectangle.

Slide 7

How can we factor trinomials such as

x2 + 7x + 12 back into binomials?

One method is to again use algebra tiles:

1) Start with x2.

Factoring Trinomials (Tiles)

2) Add seven “x” tiles (vertical or horizontal, at least one of each) and twelve “1” tiles.

3) Rearrange the tiles until they form a rectangle!

A rectangle!!!

Slide 8

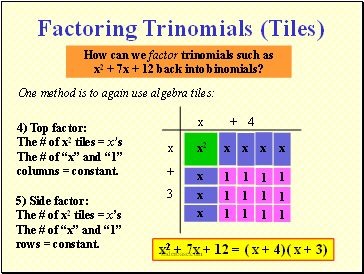
How can we factor trinomials such as

x2 + 7x + 12 back into binomials?

One method is to again use algebra tiles:

4) Top factor: The # of x2 tiles = x’s The # of “x” and “1” columns = constant.

Factoring Trinomials (Tiles)

5) Side factor: The # of x2 tiles = x’s The # of “x” and “1” rows = constant.

x2 + 7x + 12 = ( x + 4)( x + 3)

x

+ 4

x

+

3

Slide 9