Derivation Applications of Bernoulli Principal

Page
1

Slide 1

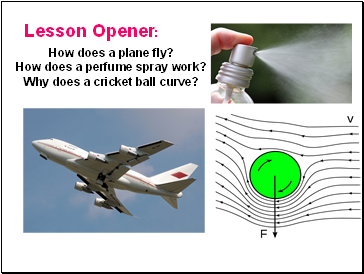
Lesson Opener

How does a plane fly?

How does a perfume spray work?

Why does a cricket ball curve?

Slide 2

Daniel Bernoulli (1700 – 1782)

Derivation and Applications of the Bernoulli Principal

NIS Taldykorgan

Grade 11 Physics

Lesson Objective:

1.To apply Bernoulli’s equation to solve problems

2.To describe Bernoulli’s principle and to derive his formula in terms of conservation of energy

3.To present applications of the Bernoulli principle

Slide 3

Bernoulli’s Principle

As the speed of a fluid goes up, its pressure goes down!

The pressure in a fast moving stream of fluid is less than the pressure in a slower stream

Fast stream = low air pressure

Slow stream = High air pressure

Slide 4

Slide 5

Equation of Continuity

Slide 6

Bernoulli’s Equation in terms of Fluid Energy

“for any point along a flow tube or streamline”

P + ½  v2 +  g h = constant

Each term has the dimensions of energy / volume or energy density.

½  v 2 KE of bulk motion of fluid

g h GPE for location of fluid

P pressure energy density arising from internal forces within

moving fluid (similar to energy stored in a spring)

Transformation of SI Units to Joule/meter3= energy/volume:

P [Pa] = [N m-2] = [N m m-3] = [J m-3]

½  v2 [kg m-3 m2 s-2] = [kg m-1 s-2] = [N m m-3] = [J m-3]

 g h [kg m-3 m s-2 m] = [kg m s-2 m m-3] = [N m m-3] = [J m-3]

Slide 7

Deriving Bernoulli’s starting with the law of continuity

Slide 8

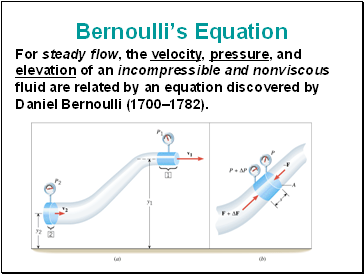
Bernoulli’s Equation

For steady flow, the velocity, pressure, and elevation of an incompressible and nonviscous fluid are related by an equation discovered by Daniel Bernoulli (1700–1782).

Slide 9

Deriving Bernoulli’s equation as Conservation of Energy

Slide 10

Bernoulli’s equation:

Slide 11

BERNOULLI’S EQUATION

In a moving fluid p+½rV2 = constant everywhere