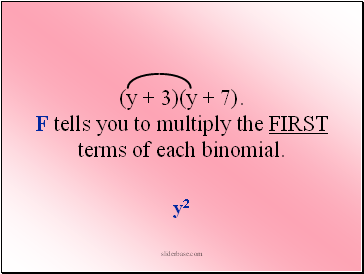Multiply two polynomials using the FOIL method, Box method and the distributive property

Page
1

Slide 1

Objective The student will be able to:

multiply two polynomials using the FOIL method, Box method and the distributive property.

SOL: A.2b

Designed by Skip Tyler, Varina High School

sliderbase.com

Slide 2

There are three techniques you can use for multiplying polynomials.

The best part about it is that they are all the same! Huh? Whaddaya mean?

It’s all about how you write it…Here they are!

Distributive Property

FOIL

Box Method

Sit back, relax (but make sure to write this down), and I’ll show ya!

sliderbase.com

Slide 3

1) Multiply. (2x + 3)(5x + 8)

Using the distributive property, multiply 2x(5x + 8) + 3(5x + 8).

10x2 + 16x + 15x + 24

Combine like terms.

10x2 + 31x + 24

A shortcut of the distributive property is called the FOIL method.

sliderbase.com

Slide 4

The FOIL method is ONLY used when you multiply 2 binomials. It is an acronym and tells you which terms to multiply. 2) Use the FOIL method to multiply the following binomials: (y + 3)(y + 7).

sliderbase.com

Slide 5

(y + 3)(y + 7). F tells you to multiply the FIRST terms of each binomial.

y2

sliderbase.com

Slide 6

(y + 3)(y + 7). O tells you to multiply the OUTER terms of each binomial.

y2 + 7y

sliderbase.com

Slide 7

(y + 3)(y + 7). I tells you to multiply the INNER terms of each binomial.

y2 + 7y + 3y

sliderbase.com

Slide 8

(y + 3)(y + 7). L tells you to multiply the LAST terms of each binomial.

y2 + 7y + 3y + 21

Combine like terms.

y2 + 10y + 21

sliderbase.com

Slide 9

Remember, FOIL reminds you to multiply the:

First terms

Outer terms

Inner terms

Last terms

sliderbase.com

Slide 10

The third method is the Box Method. This method works for every problem!

Here’s how you do it. Multiply (3x – 5)(5x + 2)

Draw a box. Write a polynomial on the top and side of a box. It does not matter which goes where.

This will be modeled in the next problem along with FOIL.